Gemini向光性

The light always goes on

0%

【论文笔记】GNN之GAT：Graph Attention Networks

发表于 分类于 本文字数： 4.6k

图神经网络（GNN）是当前深度学习领域研究的焦点之一，本文提出了一种GAT（graph attention networks）网络，它使用多头的masked自注意力机制来为每个邻居节点分配不同的权重，优化了图卷积神经网络的平均加权的问题。

论文名称：Graph Attention Networks
论文作者：Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio
发表期刊：ICLR 2018 (THU-A)
研究方向：GNN 图神经网络
关键技术：Masked self Attention, Multi Attention
主要创新：将多头注意力机制应用于图神经网络，来提升特征提取效果。
下载论文 | 查看源码

论文简介

缩写释义

缩写 描述 全称
GNN 图神经网络 Graph Neural Network
GCN 图卷积网络 Graph Convolutional Network
GAT 图注意力网络 Graph Attention Network
/ 注意力机制 Attention mechanisms

研究背景

  • 图结构数据是广泛存在的且较难处理
  • 早期，为了将图数据结构适应神经网络模型，用网格化的图数据来进一步使用CNN进行特征提取。
  • 之后，尝试扩展神经网络来直接对图数据进行处理
  • 受到CNN卷积思想的启发，图卷积神经网络也被提出和不断完善，通常分为谱方法和非谱方法。
  • 此外，注意力机制被广泛应用在端到端的任务模型中，它可以提取当前处理的输入与整个输入序列相关性更高的信息，从而提升了特征提取的效果。

本文提出一种基于注意力机制的图神经网络来GAT来使神经网络可以更高效的提取节点特征。其思想是通过关注邻域，遵循self-attention策略，计算图中每个节点的隐藏表示。

算法模型 Graph Attentional Layer

Input/ Output

  • 输入：图中\(N\)个节点\(F\)个特征的集合 \[\mathbf{h}=\left\{\vec{h}_{1}, \vec{h}_{2}, \ldots, \vec{h}_{N}\right\}, \vec{h}_{i} \in \mathbb{R}^{F}\]
  • 输出：新的节点特征表示（\(F'\)为潜在基数） \[\mathbf{h'}=\left\{\vec{h'}_{1}, \vec{h'}_{2}, \ldots, \vec{h'}_{N}\right\}, \vec{h'}_{i} \in \mathbb{R}^{F'}\]

Self Attention

为了充分提取原始节点的特征信息，模型放弃了图的结构信息而运行每个节点都可以进行信息交换，同时利用 masked 自注意机制模型来注入结构信息，即对于节点\(i\)，仅计算其直接邻居\(j \in \mathcal{N_i}\)（包括节点\(i\)自身）之间的相关程度（权重系数）\(e_{i,j}\)，并利用归一化方法方便进行加权。

\(e_{i,j}\)表示节点\(j\)对节点\(i\)的重要程度，类似于打分分值，计算式如下

\[e_{i j}=a\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)\]

式中，\(\mathbf{W} \in \mathbb{R}^{F^{\prime} \times F}\)是一个参数矩阵，\(a: \mathbb{R}^{F^{\prime}} \times \mathbb{R}^{F^{\prime}} \rightarrow \mathbb{R}\)是一种自注意力机制。

然后，利用Softmax进行归一化：

\[\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}\]

在本文中，注意力机制\(a\)是一个参数为\(\overrightarrow{\mathbf{a}} \in \mathbb{R}^{2 F^{\prime}}\)的前馈神经网络，且利用LeakyReLU作激活函数，故权重系数也可写做：

\[\alpha_{i j}=\frac{\exp \left(\text { Leaky } \operatorname{ReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\text { LeakyReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)}\]

式中，\(·T\)代表转置，\(\|\)表示连接操作。

通过上述运算，我们得到了节点\(i\)与其邻居\(j\)的注意力权重\(e_{i,j}\)。之后进行加权求和，从而得到节点\(i\)的特征输出：

\[\vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)\]

式中，\(\sigma\)是激活函数。

Multi-head Attention

为了进一步提升注意力机制的性能，GAT利用了多头注意力机制，即\(K\)个注意力机制分别独立执行相应操作，然后将它们的输出连接起来生成最终输出：

\[\vec{h}_{i}^{\prime}=\|_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)\]

式中，\(\alpha_{ij}^{k}\)表示第\(k\)个注意力机制\(a_k\)计算出的归一化注意力系数，\(\mathbf{W}^k是该注意力机制的参数矩阵\)。注意到，在多头注意力机制下，最终输出中每个节点的特征数量为\(KF'\)

特别地，如果在预测层（即Softmax上一层）执行多头注意力机制，将使用平均方法来代替连接操作：

\[\vec{h}_{i}^{\prime}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)\]

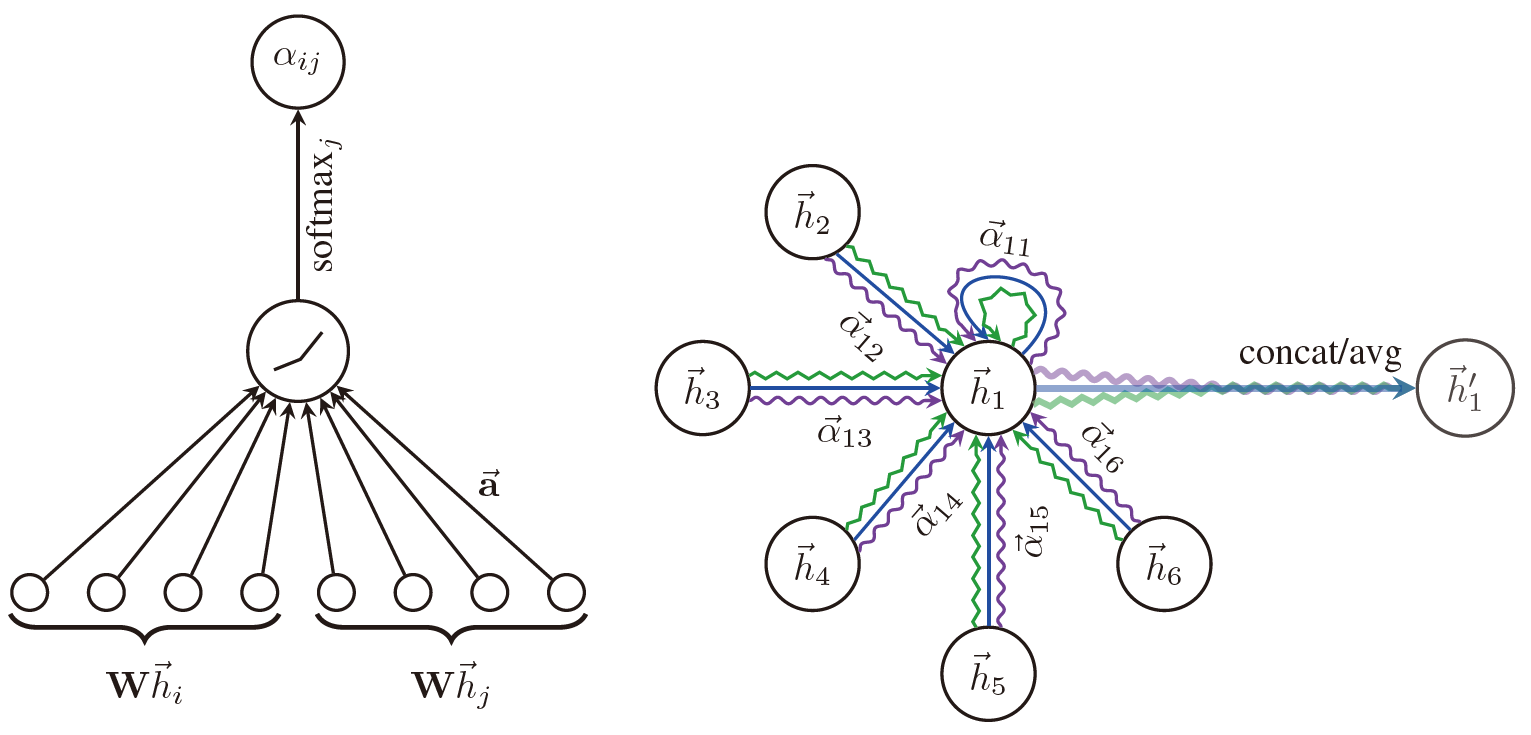
上图描述了连接操作和平均方法的基于多头注意力机制的GAT。

左图中，注意力机制\(a(\mathbf{W}\vec{h_i},\mathbf{W}\vec{h_j})\)分为两步：

  1. 线性加权得到注意力权值，即用神经网络参数\(\overrightarrow{\mathbf{a}}^{T}\)与\(\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\)相乘

\[e_{i,j} = \overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\]

  1. 非线性激活进行归一化，即用softmax对注意力权值进行归一化

\[\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}\]

  1. 加权求和得到最终输出，即用归一化注意力权值对各节点信息进行加权

\[\vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)\]

右图中，有三条不同颜色的线分别代表三个注意力机制在节点\(i\)处得到的结果，即此处\(K=3\)。之后，进行连接操作或平均操作得到最终输出\(\vec{h}'\)。

模型改进

  • 计算高效。无需使用特征值分解等复杂的矩阵运算，且操作基本都可以实现并行。

  • 可为同一个邻居的节点分配不同的重要性，提高模型表达能力。此外，注意权重可能有助于提高解释能力。

  • 注意机制以共享的方式应用于图中的所有边，因此它不依赖于对全局图结构或需预先访问其所有节点的。我们无需访问整个图，而只需要访问所关注节点的邻节点即可。这一特点的作用主要有：a) 图不需要是无向的（如果边j→i不存在，我们可以省略计算αij）。 b) 它使我们的技术直接适用于归纳学习，包括在训练过程中完全看不见的图形上评估模型的任务。

  • 它是建立在所有邻节点上的，而且无需假设任何节点顺序

  • GAT可以被看作是MoNet的一个特例。特殊地是，不同于MoNet实例相比，本文模型使用节点特征进行相似性计算，而不是节点的结构属性（假设预先知道图形结构）。具体来说，可以通过将伪坐标函数（pseudo-coordinate function）设为\(u(x,y)=f(x) \| f(y)\)，其中\(f(x)\)表示节点\(x\)的特征，\(\|\)；相应的权重函数则变成了\(w_j(u)=softmax(MLP(u))\)。

性能评估

数据集

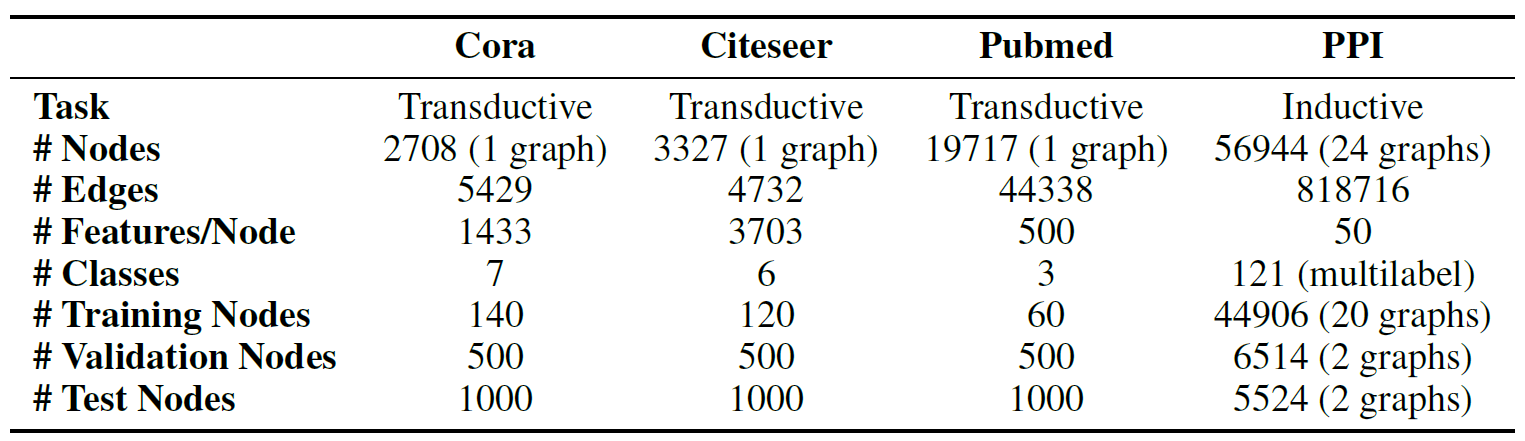
测试任务

转导学习（Transductive Learning）

先观察特定的训练样本，然后对特定的测试样本做出预测（从特殊到特殊），这类模型如k近邻、SVM等。

使用了三个标准的引证网络数据集——Cora、Citeseer与Pubmed。在这些数据集中，节点对应于文档，边（无向的）对应于引用关系。节点特征对应于文档的BoW表示。每个节点拥有一个类别标签（在分类时使用softmax激活函数）。

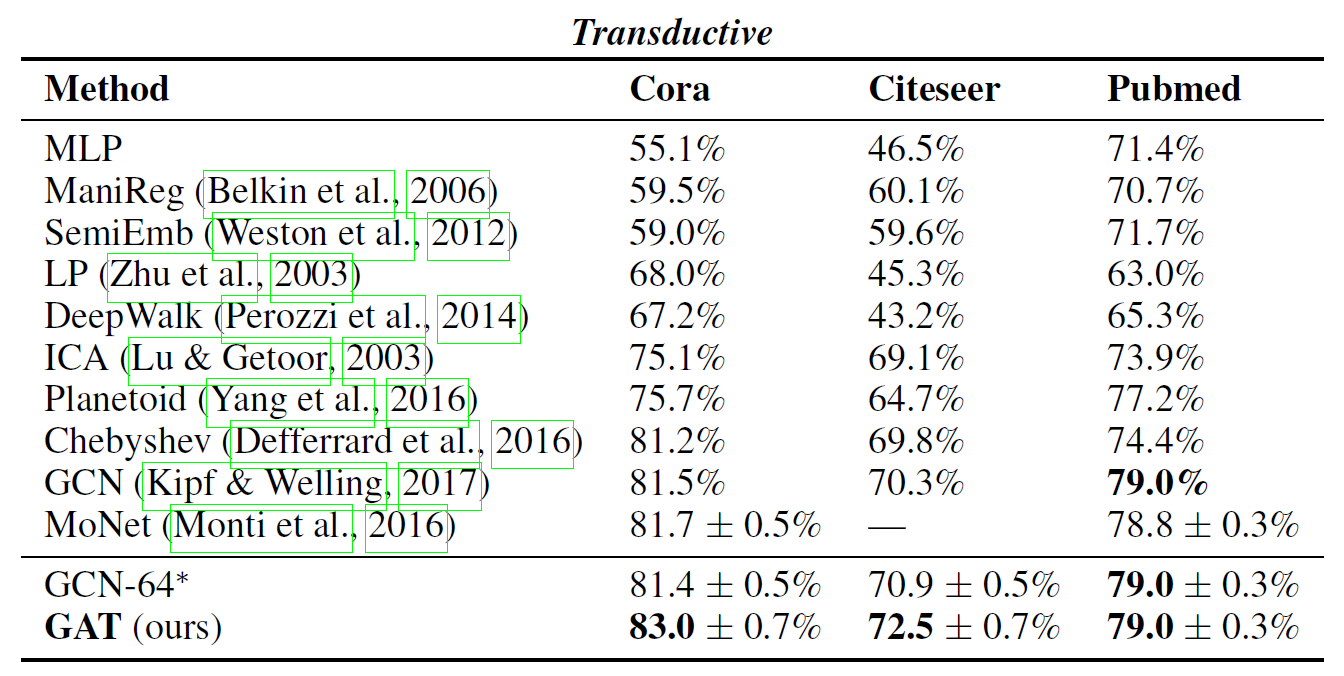
归纳学习（Inductive Learning）

先从训练样本中学习到一定的模式，然后利用其对测试样本进行预测（即首先从特殊到一般，然后再从一般到特殊），这类模型如常见的贝叶斯模型。

本文使用了一个蛋白质关联数据集（protein-protein interaction, PPI），在其中，每张图对应于人类的不同组织。此时，使用20张图进行训练，2张图进行验证，2张图用于测试。每个节点可能的标签数为121个，而且，每个节点可以同时拥有多个标签（在分类时使用sigmoid激活函数）

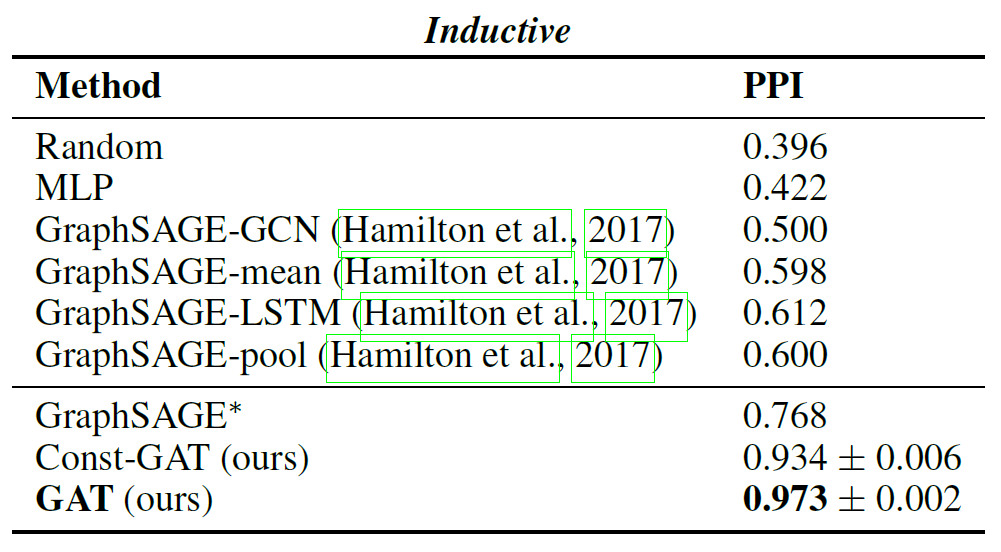
评估指标

总结思考

  • 多头注意力机制的应用：为每个邻接节点赋予不同的注意力权重，提升特征提取效果
  • 不依赖全局图结构：GAT模型无需了解整个图结构，只需知道每个节点的邻节点即可
相关文章